Épisodes de croissance cristalline rapide dans les pegmatites

 Auteurs de cette article scientifique :

1.    Department of Earth, Environmental and Planetary Sciences, Rice University, Houston, TX, 77005, USA
Patrick R. Phelps et Cin-Ty A. Lee

    2.    Department of Earth and Planetary Sciences, University of California, Riverside, CA, 92521, USA
Douglas M. Morton


Abstrait :

Les pegmatites sont des intrusions magmatiques peu profondes et à gros grains avec des cristaux approchant parfois des mètres de long. Par rapport à leurs hôtes plutoniques, on pense que les pegmatites se sont refroidies rapidement, ce qui suggère que ces gros cristaux ont dû croître rapidement. Les taux de croissance et les conditions restent cependant mal limités. Ici, nous étudions les cristaux de quartz et leurs compositions en oligo-éléments à partir de cavités miarolitiques dans la pegmatite de Stewart dans le sud de la Californie, aux États-Unis, pour quantifier les taux de croissance des cristaux. Les concentrations en oligo-éléments s'écartent considérablement de l'équilibre et sont mieux expliquées par les effets cinétiques associés à une croissance cristalline rapide. La théorie de la croissance cinétique des cristaux est utilisée pour montrer que les cristaux se sont accélérés à partir d'un taux de croissance initial de 10^-6 – 10^-7  m.s^-1 à 10^-5 – 10^-4  m.s^-1 (10 – 100 mm.jour^-1 à 1 – 10 m.jour^-1 ), indiquant que des cristaux de la taille d'un mètre auraient pu se former en quelques jours, si ces taux sont maintenus tout au long de la formation de pegmatite. Les taux de croissance rapides exigent que les cristaux de quartz se développent à partir de couches limites chimiques minces (à l'échelle du micron) aux interfaces fluide-cristal. Un composant d'advection fort est nécessaire pour maintenir de telles couches limites minces. On montre que des conditions turbulentes (nombre de Reynolds élevé) dans ces cavités miarolitiques existent pendant la cristallisation, ce qui suggère que l'exsolution volatile, la cristallisation et la génération de cavités se produisent ensemble.

Introduction

Il y a, cependant, des observations qui suggèrent que la compréhension ci-dessus de la croissance des grains dans la nature n'est pas si simple. Par exemple, il n'est pas rare de trouver des roches ignées avec des cristaux de feldspath (par exemple, des mégacrystes) de plusieurs cm à même 10 cm de taille dans des plutons peu profonds (par exemple, des porphyres), qui, vraisemblablement, refroidissent plus rapidement que leurs homologues plus fins et plus profonds⁴ . Plus frappant encore, des cristaux de taille décimétrique à même mètre caractérisent les systèmes pegmatitiques, mais les petites tailles des corps de pegmatite suggèrent que les systèmes se refroidissent rapidement ^{5 , 6} . Bon nombre des plus gros cristaux de la Terre semblent donc se trouver dans des systèmes apparemment de courte durée ⁷. Les cristaux sont-ils plus gros parce qu'ils ont eu plus de temps pour se développer, ou représentent-ils une croissance cristalline anormalement rapide? Dans ce dernier cas, quelles conditions favorisent une croissance cristalline rapide, et ces conditions pourraient-elles être plus répandues qu'on ne le pense actuellement?

Dans bon nombre de ces systèmes, l'eau peut jouer un rôle crucial dans l'augmentation de la croissance des céréales. Pour les pegmatites granitiques, l'eau est essentielle pour réduire les viscosités à l'état fondu et les températures de cristallisation tout en améliorant le transport en fusion, ce qui permet une cristallisation à des températures beaucoup plus basses ⁸ . Ici, nous montrons que les cristaux à l'échelle centimétrique de stade avancé se sont développés en quelques heures. Si de tels taux de croissance peuvent être maintenus, des cristaux de taille décimétrique à mètre dans les systèmes pegmatitiques pourraient avoir grandi en quelques jours, la croissance se produisant dans des conditions hautement dynamiques plutôt que statiques. Nous suggérons que les cristaux se sont développés à partir d'une phase fluide libre dans un système convectif turbulent.

Résultats

La pegmatite de Stewart

Pour explorer les taux de croissance des cristaux dans les systèmes naturels, nous avons mené une étude de cas sur les cristaux de quartz de la pegmatite de Stewart dans le district de Pala, dans le sud de la Californie, aux États-Unis. Les pegmatites de ce district sont âgées du Crétacé et se présentent sous forme de digues encaissées dans des plutons gabbroïques du même âge ^{9 , 10}. On pense que les pegmatites représentent des fluides de stade avancé fractionnés à partir d'un pluton gabbroïque hydraté qui forment alors un corps de pegmatite tabulaire à zonage de composition ⁹. À son plus large, le corps de Stewart est représenté par une digue de 50 m de large avec les couches extérieures composées de granit riche en feldspath (les zones intermédiaires supérieure et inférieure), une zone de perthite de transition et un noyau interne à gros grains contenant du spodumène, lépidolite, heulandite, pétalite et albite (Fig. 1). Des structures verticales (cheminées), qui contiennent de nombreuses cavités miarolitiques, émanent du noyau interne, pénétrant vers le haut dans la zone perthite. Les cheminées abritent d'abondantes tourmalines et d'albite à grains de cours, avec des cristaux de tourmaline dans certains cas approchant des dizaines de centimètres de longueur.

Dans ces cheminées, les tourmalines sont placées dans une matrice à grain plus fin d'albite, de quartz et de lépidolite, la base des cheminées étant riche en lépidolite. Les cristaux de quartz dans les cheminées, en particulier dans les cavités miarolitiques, sont souvent euhédriques. Les contacts entre les cheminées et le corps de pegmatite sont nets, ce qui suggère que les cheminées représentent des fluides de stade avancé qui ont endigué dans une zone supérieure principalement solidifiée du corps de pegmatite.Ces cheminées constituent ~ 50% en volume de la zone perthite et représentent ainsi une phase importante dans l'évolution pétrogénétique de la pegmatite⁹ . Sur la base de modèles de refroidissement conducteur, Webber et al. ⁶ suggèrent que le corps pegmatitique a refroidi de 650 ° C à moins de 550 ° C dans les ~ 9 ans après la mise en place. Il s'agit d'une limite supérieure des échelles de temps de refroidissement (et d'une limite inférieure des taux de croissance des cristaux) car tout refroidissement par convection, qui n'a pas été pris en compte par Webber et al. ⁶ , réduirait les délais de refroidissement estimés. Les taux de croissance cristalline déduits de la durée de vie thermique de la pegmatite seraient également sous-estimés car la croissance cristalline se produit à différents stades de l'évolution thermique de la pegmatite.

Fig. 1: Croquis de la pegmatite de Stewart avec une image d'une cavité miarolitique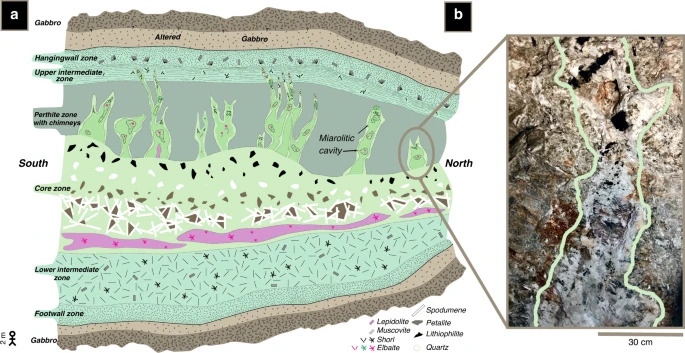


a Diagramme schématique de la pegmatite de Stewart modifiée d'après Morton et al. ⁹ . Une personne de 2 m de haut pour l'échelle en bas à gauche. Les zones externes et intermédiaires sont de composition granitique.
b Un exemple de petite cavité miarolitique (cheminée) qui s'est propagée de la zone centrale à la zone supérieure solidifiée. La cavité miarolitique contient des cristaux de tourmaline et de quartz dans une matrice à grains fins de lépidolite. Les marges plus claires de la cavité sont définies par l'albite blanche.

Nous avons étudié les cristaux de quartz euhédriques des cavités miarolitiques pour limiter les taux de cristallisation. Les quartz de ces cavités sont transparents, euhédriques (doublement terminés) et mesurent de quelques cm à 10 cm. Leurs formes euhédriques indiquent qu'ils ont nucléé et cristallisé à partir de l'intérieur du fluide constituant les cavités miarolitiques, non par nucléation le long des parois. Ils ont la particularité d'avoir des habitudes cristallines aplaties, l'axe étant court (les accolades inclinées se référant à la famille des axes). La tourmaline semble pénétrer certains cristaux de quartz, peut-être à la suite de proliférations de quartz.

Composition de quartz

Les cristaux de quartz ont été imagés à l'Université Rice à l'aide de la microscopie à cathodoluminescence froide (CL), un type de luminescence de longueur d'onde visible induite par des électrons de haute énergie émis par une cathode froide ¹¹ . Des défauts dans le réseau cristallin provoquent une luminescence dans certains minéraux. Étant donné que les défauts sont souvent corrélés avec les substitutions d'oligo-éléments, les changements de couleur CL peuvent indirectement indiquer un changement de la concentration d'oligo-éléments ¹² . Ainsi, les changements d'intensité de CL ont été utilisés pour guider notre étude géochimique. Les cristaux ont été montés en époxy, coupés et polis. Pour l'imagerie CL, une tension d'accélération de 12 kV a été utilisée avec un courant de vide de 0,4 à 0,5 mA. L'exposition de l'appareil photo a été réglée sur 4 s pour maximiser la qualité d'image. L'image résultante pour l'un des cristaux est représentée sur la figure  2a (Voir Fig. 1 supplémentaire  pour un autre cristal de quartz CL).

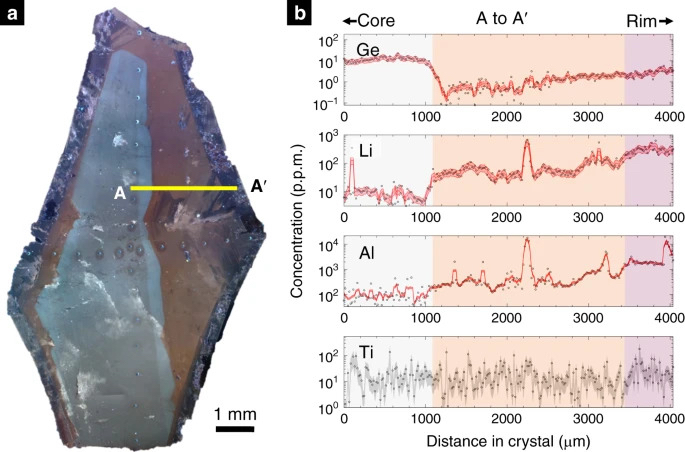
Fig. 2: Image de cathodoluminescence d'un cristal de quartz et du transect d'oligo-éléments correspondant.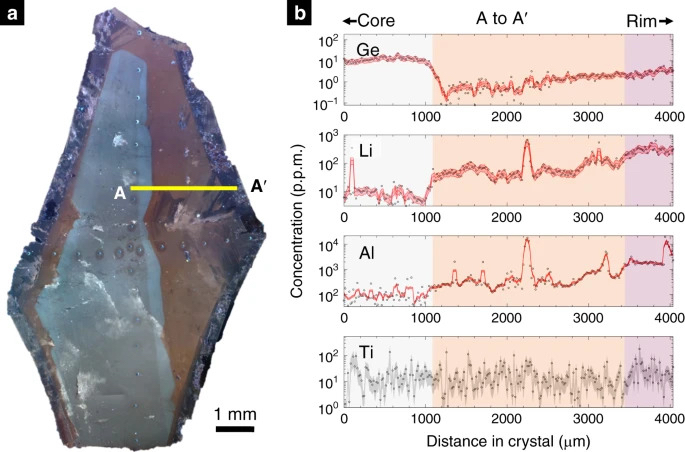


a Cathodoluminescence (CL) une image de cathodoluminescence (CL) d'un cristal de quartz de la pegmatite de Stewart. La ligne jaune représente la trace du transect géochimique. Le plan du cristal fait partie de {1000}.
b Transect géochimique A – A ′ pour Ge, Li, Al et Ti en ppm poids. Les points représentent les données et les lignes rouges représentent les moyennes mobiles. Les enveloppes rouges représentent l'erreur standard de la moyenne basée sur 3 σ d'analyses ponctuelles et une moyenne mobile à trois points. L'enveloppe grise en Ti représente 1 écart type par rapport aux points de données. Les valeurs d'erreur sont respectivement de 26%, 28%, 8,5% et 57% pour Ge, Li, Al et Ti. Les couleurs d'arrière-plan correspondent aux couleurs CL dans a . Ti est dispersé car les mesures sont proches des limites de détection.

Les compositions des oligo-éléments ont été quantifiées en utilisant un système d'ablation laser New Wave 213 nm couplé à une spectrométrie de masse à plasma à couplage inductif à secteur magnétique ThermoFinnigan Element 2 (ICP-MS) à l'Université Rice. Des analyses de points laser et des transects linéaires ont été réalisés. Les transects ont été réalisés en utilisant un diamètre de spot de 110 μm avec une fluence de ~ 13 J m^-2 , un taux de répétition de 5 Hz et une vitesse laser latérale de 9 μm s^-1 . La grande taille du spot limite la résolution spatiale de nos transects à 100–200 μm. Les analyses ont été effectuées en mode de résolution de masse moyenne ( m / Δ m  = 3000). Les masses suivantes ont été mesurées: Li⁷ , Na²³ , Mg²⁵ , Al²⁷ , Si³⁰, P³¹ , K³⁹ , Ti⁴⁹ , Zn⁶⁶ , Ga⁶⁹ , Ge⁷³ et Ge⁷⁴. Les signaux ont été corrigés en arrière-plan, normalisés à Si³⁰ et convertis en concentrations en utilisant du verre synthétique NIST 612¹³ et deux obsidiennes rhyolitiques naturelles M3–33 et M3–86¹⁴ comme étalons externes et forçant la somme de tous les métaux mesurés (sous forme d'oxyde) égal à 100%.

Trois cristaux de quartz ont été cartographiés en utilisant CL. La CL d'un cristal est représentée sur la figure  2a et est représentative des zones de couleur vues dans CL à partir de la pegmatite. En CL, les quartz se composent de trois zones nettement délimitées: une zone de noyau blanche, une zone médiane orange et un bord extérieur violet. Le noyau blanc se compose de deux zones internes subtiles: une zone interne plus sombre entourée d'un manteau fin et légèrement plus brillant. Nous considérons ces deux zones comme des parties internes de la zone centrale car leurs couleurs CL ne sont que subtilement différentes. Dans tout le grain, une luminescence bleue transitoire principalement dans les zones orange et violette, qui peut être liée à des réarrangements induits par le faisceau d'électrons d'oligo-éléments alcalins à l'échelle nanométrique^15,16, a été observée.

Une composition représentative transect (A-A ') à travers les trois zones CL est représentée sur la Fig.  2b (voir les figures supplémentaire.  Deux - sept pour d' autres transects). Les transitions de couleur ou d'intensité de CL sont corrélées à de larges changements dans les concentrations en oligo-éléments¹². Dans la région de noyau blanc, la plupart des éléments montrent une variation minimale avec la distance (aucun changement de composition ne se produit à travers la transition CL interne dans la zone de noyau blanc discutée ci-dessus). Par exemple, dans la zone du noyau blanc, Li et Al sont relativement constants, tandis que Ge augmente vers l'extérieur de 10 à ~ 20 ppm avant de redescendre à 10 ppm Au contact entre le noyau blanc et la zone médiane orange, des diminutions marquées de Ge et des augmentations dans Al et Li sont observés. Dans la zone médiane orange, Ge, Al et Li montrent une augmentation graduelle des concentrations vers l'extérieur, ponctuée de pics en Al et Li dus à des inclusions (confirmées optiquement mais de minéralogie inconnue en raison de leur petite taille). Au contact entre la zone extérieure médiane orange et violette, Al et Li augmentent nettement, mais aucun changement brusque n'est observé dans Ge. Dans la zone extérieure violette,Al et Li s'aplatissent rapidement et diminuent même légèrement, tandis que Ge continue d'augmenter.

Les concentrations de Ti dans la zone centrale du cristal sont proches des limites de détection et se situent dans une constante d'erreur comprise entre 10 et 15ppm. En supposant une activité TiO₂ de 0.6 (pas de phases d'appui du Ti) et 2 kbar, on arrive à ~ 600°C en utilisant le thermomètre de Wark et Watson¹⁷ . Les thermomètres de Huang et Audétat¹⁸ et Thomas et al.¹⁹ tiennent compte de la dépendance à la pression, abaissant la température entre 460¹⁹ et 540°C¹⁸ . L'adoption d'une activité TiO₂ plus faible donnerait des températures plus élevées, mais si les teneurs en TiO₂ sont élevées en raison de la croissance rapide des cristaux (voir ci-dessous), des températures plus basses seraient estimées. Bien que nous ne puissions pas obtenir une température exacte pour la formation de ces quartz, il semblerait que les quartz se soient formés à des températures non> 540°C.

Contrôle cinétique versus contrôle externe sur le zonage compositionnel
Nous interprétons les transitions CL comme reflétant les différences originales dans la densité des défauts ou des impuretés d'oligo-éléments associées à des changements soudains du taux de croissance des cristaux. Les profils de concentration Li, Ge et Al plus larges à travers les zones CL pointues sont plus grands que la résolution spatiale de la taille de notre spot laser et peuvent suggérer une relaxation diffusive de ces éléments. Cependant, la largeur de chacun de ces profils de concentration est similaire, ce qui se reflète dans le fort couplage des concentrations de Li et d'Al (Fig.3). La similitude dans les échelles de longueur de ces transitions, si elle est liée à la diffusion, est inattendue car ces éléments ont des diffusivités nettement différentes. Par exemple, à des températures de ~ 600°C, les diffusivités du traceur dans le quartz sont de 5×10^-12  m².s^-1 (d'après Verhoogen²⁰ ) pour Li, 3×10^-23 m².s^-1 pour Al (Tailby suivant et al.²¹ ), et ~ 1×10^-32 m².s^-1 pour Ge (en supposant Ge se comportant de même que Si en autodiffusion²²). En particulier, la diffusivité extrêmement faible de Al nécessiterait près de 2 My pour générer les profils d'Al par diffusion en supposant un profil de fonction d'étape initial - bien plus longue que la durée de vie de la pegmatite. Aucune relaxation diffuse n'est donc prévue pour Ge et Al.

Fig. 3: Al contre Li dans le quartz.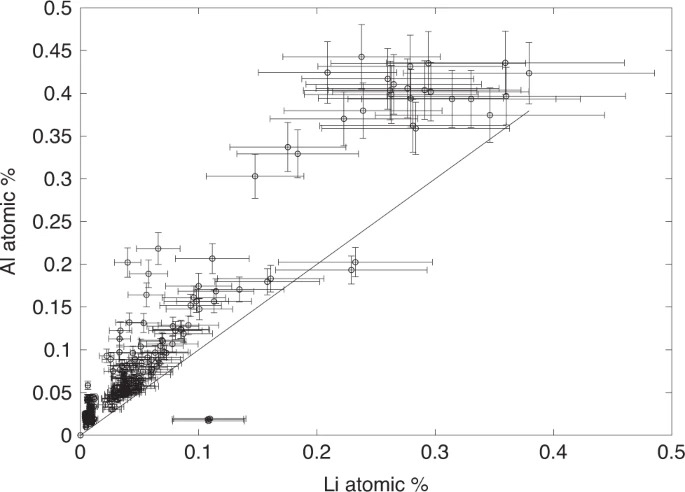

La ligne représente une correspondance 1: 1 de Li et Al. La corrélation de Li avec Al indique un couplage de charge possible. D'autres cations monovalents, tels que Na, peuvent représenter l'Al restant. Les barres d'erreur sont de 3σ en fonction de la précision de mesure interne.


Cependant, la diffusivité vraisemblablement élevée de Li devrait prévoir une relaxation diffusive mesurable. Par exemple, au cours de la durée de vie de la pegmatite (~ 9 ans), Li aurait dû se diffuser sur une échelle de longueur de 7,5 cm, plus grande que la taille des cristaux de cette étude. Cependant, le fait que Li est fortement corrélé avec Al suggère que Li⁺ dans le quartz est couplé en charge avec Al³⁺ , ce qui suggère que les diffusivités publiées des traceurs de Li peuvent ne pas être applicables. Au lieu de cela, Li pourrait diffuser aussi vite que Al en raison du couplage de charge. La possibilité que le Li diffuse très lentement est en contradiction avec certaines études qui ont déduit des temps de séjour courts des cristaux dans les systèmes magmatiques à partir des profils de concentration de Li²³. Nos résultats sont similaires à l'observation d'une diffusion très lente du Li dans les zircons en raison du couplage avec des éléments de terres rares à diffusion lente²⁴. Le fort couplage de Li à Al et Ge à diffusion lente déduit ici suggère qu'il peut y avoir eu une relaxation diffusive sous-solide limitée de Li, Al et Ge à travers ces limites.

L'origine des différences de composition entre et au sein de chaque zone CL est donc intéressante. Les possibilités comprennent des changements dans la composition du fluide (forçage externe) ou des changements dans la nature de la croissance cristalline (processus internes). Pour les raisons suivantes, nous ne favorisons pas les changements de composition des fluides en tant que moteur principal. Bien que les concentrations de quartz Ti (variant de 10 à>50 ppm, selon l'emplacement dans les cristaux) dans cette étude soient similaires à celles du quartz provenant de plutons granitiques, les concentrations d'Al (> 1000 ppm) sont nettement plus élevées que celles du quartz provenant de plutons granitiques. et la plupart des pegmatites (Fig.4). Étant donné que Al est hautement incompatible dans le quartz²⁵, ces concentrations en Al remarquablement élevées nécessiteraient des fluides ou des fondants avec des teneurs en Al déraisonnablement élevées. On note également que la composition en oligo-éléments des magmas ou des fluides en différenciation doit évoluer de manière prévisible: la cristallisation progressive conduit à un enrichissement en éléments incompatibles et à l'épuisement des éléments compatibles. Li et Al sont incompatibles dans le quartz^25,26. Ge est similaire à Si^27,28,29 et devrait donc être compatible dans le quartz, comme le confirment He et al.³⁰. Li et Al doivent donc être systématiquement anticorrélés avec Ge, si leurs concentrations sont contrôlées par un fluide ou magma subissant un fractionnement cristallin. Au lieu de cela, la relation de Li et Al avec Ge dans tout le grain de quartz montre plus de complexité.

Fig. 4: Concentrations Ti versus Al dans le quartz des granites et pegmatites.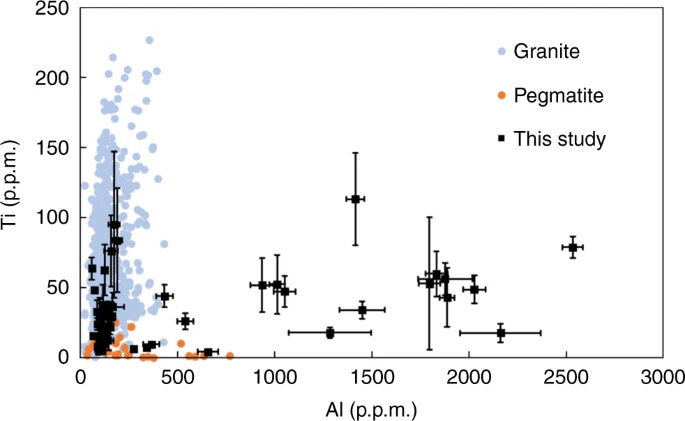

Les données granitiques compilées à partir d'Ackerson et al.⁶⁰ et les données sur la pegmatite de Garate-Olave et al.⁶¹ et Götze et al.¹⁵. Les barres d'erreur représentent 3 σ . Les données de cette étude proviennent d'analyses ponctuelles.


Alors que la possibilité de changements externes dans la composition du fluide ne peut pas être complètement exclue, l'adoption d'une telle hypothèse exigerait non seulement des compositions de fluide très inhabituelles, mais des changements très importants et soudains de la composition du fluide. Pour ces raisons, nous explorons également la possibilité que les compositions d'oligo-éléments reflètent des processus cinétiques, en particulier les effets d'une croissance cristalline rapide.

Discussion

Dans cette section, nous explorons comment les changements dans le taux de croissance des cristaux peuvent affecter la façon dont les oligo-éléments sont incorporés dans les cristaux^31,32,33. Un oligo-élément se répartira en un minéral en fonction de son coefficient (k) de partage à l'équilibre, qui est la concentration dans le cristal divisée par la concentration dans le milieu de croissance (fluide ou liquide) immédiatement adjacent à la surface cristalline en croissance à l'équilibre ( k  =  C_s / C_l ). Cependant, si le cristal croît à des taux comparables ou plus rapides que ce que l'élément peut diffuser dans le fluide, une couche limite chimique dans le fluide se développe près de l'interface cristal-fluide en progression (Fig.5). Pour un élément incompatible (k <1), la croissance cristalline conduit au rejet de l'élément du cristal et à l'enrichissement ultérieur de l'élément dans la couche limite fluide. L'inverse est vrai pour les éléments compatibles (k >1), dans lequel l'incorporation préférentielle de l'élément dans le cristal conduit à une couche limite chimique appauvrie dans le fluide. Qualitativement, la largeur de la couche limite est contrôlée par les taux relatifs de croissance cristalline et d'homogénéisation diffusive ou advective dans le fluide. Par exemple, une croissance cristalline rapide par rapport à la diffusion dans le fluide se traduira par des couches limites chimiques extrêmement enrichies et étroites pour les éléments incompatibles (et des couches limites extrêmement appauvries et larges pour les compatibles). Si les échelles de temps de diffusion dans le cristal sont plus longues que les échelles de temps de croissance des cristaux, le zonage des cristaux reflétera les changements dans la composition de la couche limite, et non la composition du fluide de champ lointain ou du milieu de croissance magmatique.

Fig. 5: Réponse des oligo-éléments due aux changements du taux de croissance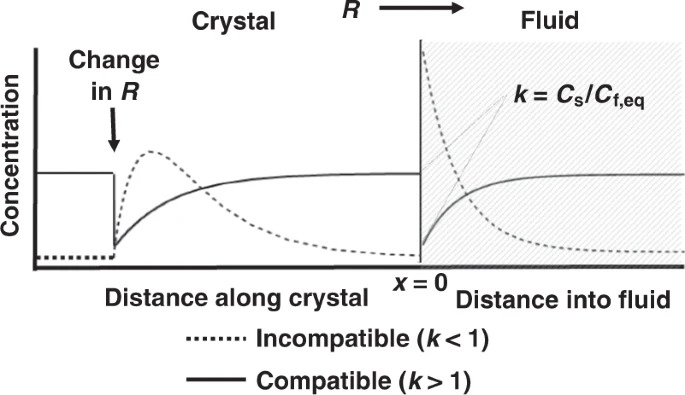
Un diagramme conceptuel montre comment le taux de croissance des cristaux (R) affecte les distributions d'éléments traces associées à un changement soudain du taux de croissance. La figure montre le cas transitoire dans lequel le taux de croissance augmente soudainement à partir d'un état stationnaire précédent. La concentration (C) dans le fluide près du cristal augmente ou diminue, en fonction de la compatibilité de l'élément (k, le rapport d'équilibre de la concentration solide à la concentration liquide), qui est enregistrée dans le cristal comme un enrichissement ou une déplétion dans le cristal , respectivement. Si le taux de croissance reste constant, la concentration de fluide atteindra éventuellement un nouvel état d'équilibre, qui se traduira par une constante C dans le cristal en fonction de la distance, car la distance représente le temps. Le profil de concentration dans le fluide à l'état stationnaire représentera une couche limite chimique statique.

Ces concepts peuvent être placés dans un cadre quantitatif suivant un modèle d'advection-diffusion avec l'interface cristal-liquide comme référentiel mobile^{31, 33,34,35}

Voir la source de l'article pour les équations de calculs de croissance (Bas de page).


Sur la figure  6 , nous comparons les concentrations de Ge et d'Al aux valeurs modélisées de Ge et Al à l'état d'équilibre pour différentes valeurs de Rδ (équation 4), c'est-à-dire le produit de la vitesse de croissance des cristaux et de l'épaisseur de la couche limite. Nous avons supposé une diffusivité constante de sorte que les variations de Rδ représentent effectivement les changements du nombre de Peclet. À l'état stationnaire, on s'attend à ce que δ soit une constante pour un taux de croissance cristallin et une diffusivité donnés (et une advection de fluide), mais comme nous considérons des changements dans R, nous ne savons pas a priori ce qu'est δ, donc Rδ varie. Dans tous les cas, les augmentations de Rδ reflètent très probablement une augmentation du taux de croissance.

Fig. 6: Comparaison des profils mesurés avec les concentrations modélisées à l'état d'équilibre.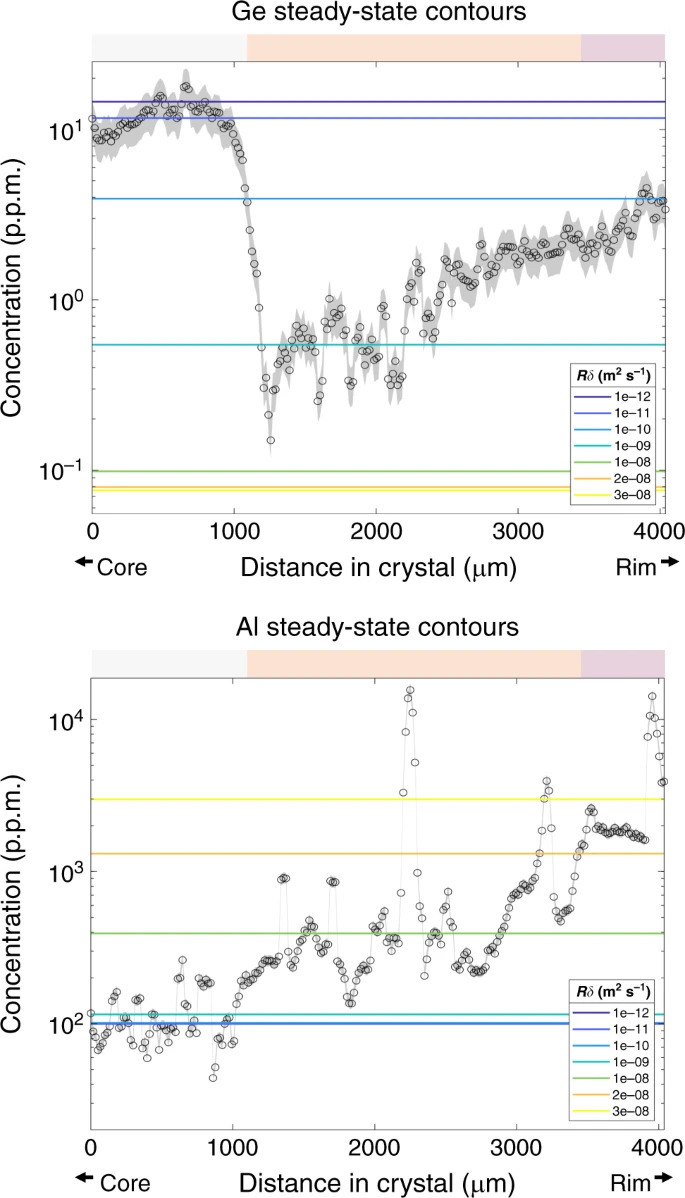

Concentrations à l'état d'équilibre calculées à l'aide de l'Eq. 4 pour différents Rδ et une constante D de 8×10^-9  m² .s^-1 pour Ge et Al. Les données de Ge et d'Al vers le noyau du cristal correspondent à un R δ similaire , suggérant une croissance en régime permanent dans le noyau. Au-delà de la région centrale, Ge et Al donnent des Rδ différents , suggérant un état transitoire. Les valeurs Rδ inférieures (10^-10 à 10^-12  m² .s^-1) dans le graphique Al sont presque identiques, ce qui les amène à tracer les uns sur les autres. La barre de couleur horizontale correspond aux régions de couleur CL. Les enveloppes d'erreur représentent l'erreur standard de la moyenne basée sur 3 σ d'analyses ponctuelles et une moyenne mobile à trois points. Les valeurs d'erreur sont respectivement de 26% et 8,5% pour Ge et Al.


Dans la région centrale, les teneurs en Ge sont élevées et les teneurs en Al sont faibles, comme prévu car Ge est compatible et Al incompatible. Nous trouvons que les concentrations de Ge et d'Al dans le cœur peuvent toutes deux être modélisées par Rδ de 10^-11 à 10^-12  m².s^-1. En revanche, dans la partie extérieure du cristal, Ge et Al augmentent. Si des solutions en régime permanent sont supposées, une augmentation de Rδ est nécessaire pour correspondre à l'augmentation de Al, tandis que des diminutions de Rδ sont nécessaires pour correspondre aux données Ge.

En résumé, nos observations suggèrent que le cristal se développait initialement dans des conditions d'équilibre (zone blanche du noyau), mais a ensuite subi un changement soudain de taux de croissance (à la transition du blanc à l'orange). Ainsi, alors que les concentrations élémentaires centrales reflètent une croissance cristalline régulière, les profils élémentaires ultérieurs reflètent des réponses transitoires à des augmentations soudaines de la croissance cristalline.

Comme indiqué ci-dessus, les profils Ge et Al dans la partie externe du cristal sont incompatibles avec la croissance à l'état d'équilibre, et par conséquent, des conditions transitoires doivent être prises en compte. En utilisant un élément donné, le rapport entre le taux de croissance initial et le taux de croissance final peut être limité mais pas les taux de croissance absolus. Cependant, pour deux éléments ou plus, les taux de croissance peuvent être limités par l'équation.5 (avec frottis laser pris en compte dans la note supplémentaire  1 , les équations supplémentaires  1 et 2 et la fig.9 supplémentaire ), qui décrit la réponse à une augmentation instantanée du taux de croissance d'un cristal se développant initialement à l'état stationnaire. Nous appliquons cette équation à la transition de la zone de noyau blanc à la zone médiane orange parce que les profils constants observés dans la région de noyau blanc suggèrent que l'état d'équilibre a été atteint comme discuté ci-dessus.

Les deux paramètres que nous faisons varier sont le taux de croissance initial à l'état d'équilibre R_i et le taux de croissance final R_f . Nous adoptons les mêmes diffusivités évoquées ci-dessus. R_i et notre diffusivité supposée contrôlent la concentration à l'état d'équilibre dans la zone du noyau blanc, tandis que le rapport R f / R_i contrôle la forme de la réponse après une augmentation du taux de croissance. En faisant varier le taux de croissance initial entre 10^-7 et 10^-6  m.s^-1 et la croissance finale entre 10^-5 et 10^-4  m.s^-1, les comportements d'Al et de Ge peuvent être capturés (Fig.7). L'adoption de taux de croissance plus lents ( R_i = 10^-7  m.s^-1, R_f = 10^-6  m.s^-1) entraîne une réponse trop lente et ne correspondra donc pas à la courbure des données dans les limites du modèle et de son hypothèses. Adopter des débits plus rapides ( R_i = 10^-5  m.s^-1, R_f= 10^-4 m.s^-1) ne correspond pas non plus aux données, montrant des temps de réponse trop courts. Les incertitudes dans les diffusivités peuvent être expliquées en adoptant des diffusivités plus élevées ou plus faibles (d'un ordre de grandeur), entraînant respectivement des taux de croissance plus élevés et plus faibles. Si le coefficient de partage pour Al est inférieur (plus incompatible) que celui utilisé ici, nous prédisons à peu près le même profil d'éléments traces. Un coefficient de partage plus compatible (c.-à-d. 0,1) produira un profil de concentration légèrement inférieur, mais toujours dans le tableau des données.

Fig.7: Comparaison des profils mesurés avec des réponses transitoires modélisées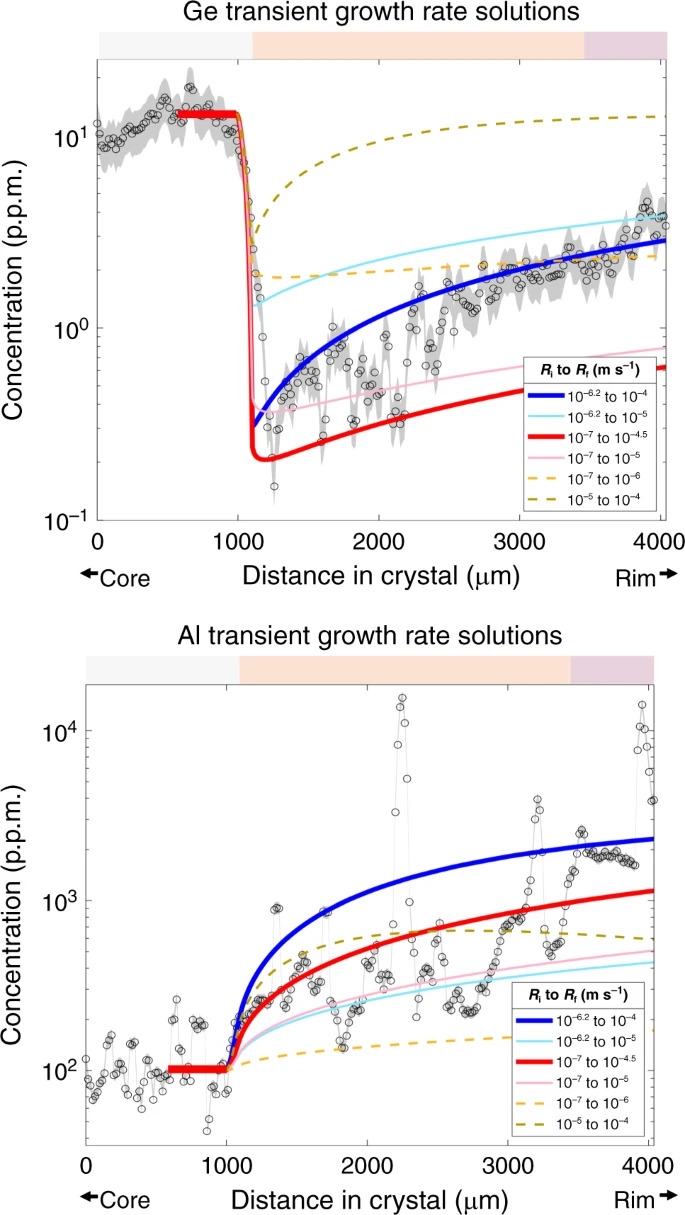

Solutions pour les réponses transitoires pour Ge et Al. Les courbes représentent la réponse pour un changement de fonction d'étape dans le taux de croissance des cristaux de R_i à R_f à ~ 1000 μm (la transition orange-blanc). Un changement d'ordre de grandeur de 2 à 2,5 du taux de croissance est nécessaire pour correspondre aux données. Al devrait finalement atteindre un pic et retomber à l'état d'équilibre, mais le cristal n'a pas poussé assez longtemps pour que cela se produise. La barre de couleur sur le dessus correspond aux zones de couleur CL dans le cristal. Les enveloppes d'erreur représentent l'erreur standard de la moyenne basée sur 3σ d'analyses ponctuelles et une moyenne mobile à trois points. Les valeurs d'erreur sont respectivement de 26% et 8,5% pour Ge et Al.

Sur la base de l'analyse ci-dessus, nous estimons que le taux de croissance a augmenté d'environ 100 fois du cœur à la jante, avec des taux de croissance initiaux de l'ordre de 10 – 100 mm.jour^-1 (10^-7 – 10^-6m.s^-1) dans la région du noyau blanc à des taux de croissance approchant 1–10 m.jour^-1 (10^-5 –10^-4  m.s^-1) dans la région médiane orange (Fig.8). Nous ne sommes pas en mesure d'estimer le taux de croissance de la zone violette externe car la zone médiane orange n'a jamais atteint l'état d'équilibre, ce qui invalide l'application de l'Eq.  5à la transition orange-violet. Cependant, la légère diminution d'Al (incompatible) et l'augmentation de Ge (compatible) dans la zone extérieure violette suggèrent une légère diminution du taux de croissance.

Fig. 8: Dessin illustrant comment les taux de croissance des cristaux peuvent avoir changé d'un noyau à l'autre.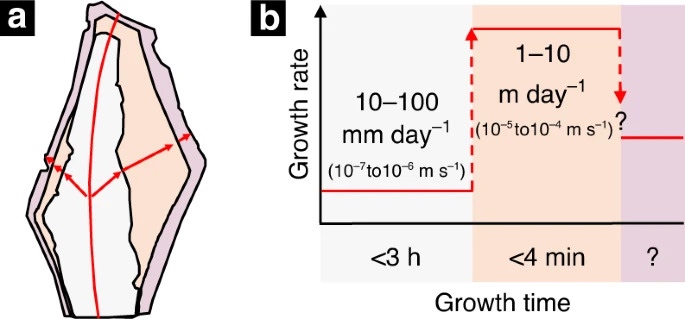

a Une esquisse de la zonation CL du cristal.
b Historique de croissance reconstitué du cristal avec des couleurs CL superposées.

Pour le contexte, ces taux de croissance des cristaux sont comparés à d'autres taux géologiques de la figure 9. Les taux de croissance du quartz pegmatitique dans cette étude sont clairement rapides par rapport aux taux de croissance déduits pour les grenats métamorphiques^45,46 et le quartz dans les granitiques plutoniques⁴⁷. On pense que les phénocristaux de quartz dans les roches volcaniques ont également augmenté rapidement^48,49, mais les taux de croissance du quartz pegmatitique sont toujours au moins aussi rapides que les taux de croissance inférés les plus rapides pour le quartz volcanique. Enfin, les taux de croissance des cristaux sont comparés à d'autres taux géologiques, tels que les mouvements des plaques⁵⁰ et les déformations liées aux tremblements de terre, telles que le glissement lent et le fluage asismique⁵¹(et les références y figurant). Cette comparaison nous permet de déterminer si la croissance cristalline pourrait jouer un rôle important dans d'autres systèmes. Nous notons que les échelles de temps de croissance des cristaux dans les systèmes pegmatitiques peuvent se rapprocher de celles du glissement lent et du fluage asismique, ce qui soulève la question de savoir si la croissance des cristaux peut être importante pendant le défaut ou la guérison de défaut.

Fig. 9: Comparaison des taux de croissance des cristaux de pegmatite de cette étude avec les taux d'autres processus géologiques.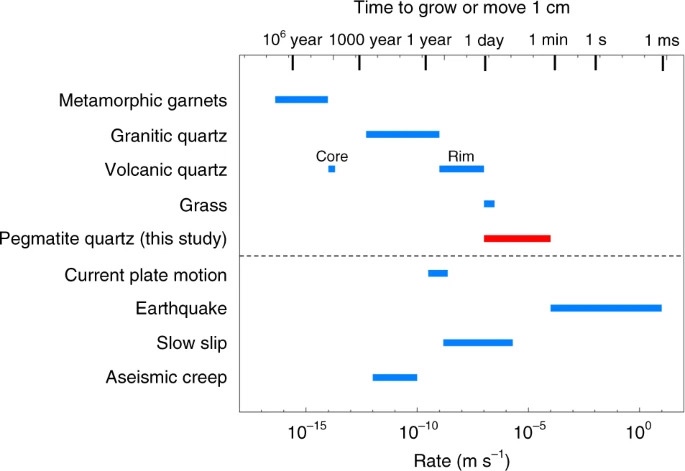

Sources de données: grenats métamorphiques^45,46 ; quartz granitique⁴⁷ ; quartz volcanique^48,49 ; herbe⁶² ; mouvements de la plaque⁵⁰ ; les taux sismiques⁵¹ (et leurs références).


Dans les systèmes d'advection, l'épaisseur de la couche limite diffusive est contrôlée par un équilibre entre la diffusion chimique dans le fluide, qui élargit la couche limite, et l'advection, qui amincit la couche limite^33,52,53. Plus la composante d'advection est forte, plus la couche limite est étroite, augmentant ainsi le gradient chimique au contact fluide-cristal et donc le flux d'éléments du fluide dans le cristal. Bien que Eq.4 a été dérivée pour un système statique, elle peut toujours être appliquée à un système dynamique en régime permanent. C'est parce que le transport chimique normal à l'interface croissante à l'intérieur de la couche limite est contrôlée par diffusion et non par advection. Ceci est analogue aux couches limites thermiques dans les systèmes à convection thermique, où l'épaisseur de la couche limite thermique à l'état stationnaire est contrôlée par un amincissement par convection, mais le transport vertical de la chaleur à l'intérieur de la couche limite est contrôlé par diffusion thermique⁵⁴. Ainsi, en utilisant les diffusivités adoptées ci-dessus et en supposant que la région centrale était proche de l'état stationnaire (nous ne pouvons pas appliquer l'équation 4 aux zones orange ou violette car elles n'ont pas atteint l'état stationnaire), nous trouvons pour la région centrale une épaisseur de couche limite de 10 –100 μm. Cela suppose un état stationnaire Rδ ~ 10^-11 – 10^-12  m². s^-1 et R ~ 10^-7  m. s^-1 pour le coeur, ce dernier contraint en modélisant la réponse transitoire du coeur blanc vers les zones médianes orange. Nous notons que la formulation que nous avons utilisée (Eq. 5) pour modéliser la réponse transitoire a été dérivée pour un cas statique. Dans les systèmes dynamiques, les couches limites seraient amincies, et parce que le taux de croissance évolue inversement avec l'épaisseur de la couche limite dans l'Eq.5 , nos taux de croissance estimés à partir du modèle transitoire statique sont des limites minimales. Ainsi, l'épaisseur de la couche limite dans le noyau est une limite maximale, et surtout, est considérablement plus petite que celle du cas statique (δ ~ D /R ~ 8 cm). Un amincissement progressif de la couche limite est donc nécessaire.

Dans un système d'advection, δ est lié à la vitesse du fluide⁵⁵. L'épaisseur de la couche limite chimique δ échelles inversement avec le nombre de Sherwood Sh, c'est-à-dire δ ~  L/ Sh, où L est la longueur caractéristique du cristal et Sh relie le transfert de masse par convection au transfert de masse diffusif 56 . Sh est en relation avec le nombre de Reynolds Re du fluide (voir la note complémentaire  2 avec complémentaire Eq.  3 - 5⁵⁵ et supplémentaires Tableau  1), qui se rapporte à des forces d' inertie visqueux. Re est donné par ULρ/ μ, où U est la vitesse du fluide, ρ est la densité du fluide, et μ est la viscosité du fluide⁵⁷ . L'épaisseur de notre couche limite estimée correspond à un Re de 20 à 4000 et à une vitesse moyenne du fluide de 0,1 à 20  cm.s^-1 . Étant donné que les changements de diffusivité entraînent un changement proportionnel du taux de croissance, le changement s'annulera, ce qui signifie que cette valeur est valable pour toutes les valeurs de diffusivité Ge. Étant donné que Re> ~ 2300 dans l'écoulement de la conduite est considéré comme turbulent⁵⁷ , nos cristaux de quartz peuvent avoir grandi dans un environnement hautement dynamique. Pour des conditions comparables, mais dans des systèmes de fusion de silicate, Re pour la croissance cristalline est «1 en raison des viscosités très élevées des silicates fondus.

Les pegmatites semblent se former sur des échelles de temps beaucoup plus courtes que les roches plutoniques typiques, mais paradoxalement, elles ont des cristaux beaucoup plus gros, ce qui à lui seul exige que les taux de croissance des cristaux soient beaucoup plus élevés dans les systèmes pegmatitiques que dans les systèmes plutoniques typiques. On ne sait pas exactement pourquoi, mais on pense généralement qu'une abondance de phase fluide libre est importante pour la formation de pegmatites^8,38,39. Le raisonnement est que les diffusivités dans les fluides sont plus élevées que celles des silicates fondus, permettant ainsi un flux plus rapide de nutriments vers le cristal et améliorant les taux de croissance^58,59. Cependant, une augmentation de la diffusivité seule peut ne pas suffire à réduire les temps de croissance de milliers d'années à heures car les diffusivités des cations communs dans l'eau à température élevée sont de l'ordre de 10^-8  m².s^{-1 42,43} et les diffusivités en les silicates fondus sont de l'ordre de 10^-10 m².s^-1. Comme discuté ci-dessus, le flux vers le cristal peut également être augmenté en diminuant l'épaisseur de la couche limite chimique dans le fluide par advection. Nos travaux montrent que l'épaisseur de la couche limite de ces cristaux était de ~ 10⁴ fois plus mince qu'une couche limite purement diffusive sans amincissement par advection, aboutissant finalement à une amélioration de 10⁴ fois les taux de croissance. De telles couches limites minces, comme conclu ci-dessus, ne sont maintenues que dans des conditions turbulentes.

Ces résultats peuvent éclairer la nature de la minéralisation de la pegmatite de Stewart. Nous envisageons la pegmatite issue de la mise en place de digues d'un magma silicaté hydraté dans la roche gabbro hôte. Les zones externes (supérieure et inférieure) du corps de pegmatite se sont solidifiées d'abord par refroidissement contre le gabbro hôte déjà solidifié, tandis que la zone centrale centrale s'est solidifiée en dernier lorsque le front de cristallisation progressait vers l'intérieur. Cette cristallisation progressive concentre les volatils et autres éléments / composants incompatibles dans le silicate fondu résiduel dans la zone centrale. La saturation éventuelle de ces volatils conduit à une exsolution d'une phase fluide libre et à une accumulation de surpression, déclenchant la fracturation vers le haut et le transport de la phase fluide dans la zone supérieure solide et générant des cheminées et des cavités miarolitiques.

Au fur et à mesure que le fluide se dilate dans les cavités, la décompression qui en résulte conduit à une sursaturation des constituants dissous dans le fluide, entraînant une nucléation rapide et une croissance cristalline. Les changements de pression peuvent également entraîner des changements rapides des taux de croissance. La mise en place de ces fluides dans des fractures semble s'accompagner de turbulences, ce qui augmente considérablement les taux de croissance des cristaux, permettant la formation de cristaux pegmatitiques en quelques heures. Nous envisageons donc que des cavités miarolitiques se sont formées dans des conditions hautement dynamiques et éphémères.

Nos taux de croissance cristalline ne reflètent clairement que les processus opérant dans la formation de cavités miarolitiques de stade avancé et ne s'appliquent pas à la cristallisation dans d'autres parties de la pegmatite. Des études similaires utilisant la chimie des éléments traces de cristaux dans différentes parties d'un corps de pegmatite devraient être mesurées à l'avenir pour mieux comprendre comment les taux de croissance des cristaux varient au cours de toute l'histoire d'une pegmatite. En résumé, nos résultats suggèrent qu'il peut être utile de reconsidérer si les gros cristaux dans d'autres systèmes magmatiques, tels que les porphyres, sont la conséquence d'une croissance rapide plutôt que d'une croissance lente sur de longues périodes d'incubation.

Méthodes

Voir la source pour l’équation de référence utilisé (Bas de page).

Références

    1.    1.Winkler, HGF Cristallisation du magma basaltique comme enregistré par variation de la taille des cristaux dans les digues. Minéral. Mag. J. Mineral. Soc. 28 , 557–574 (1949).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    2.    2.Brandeis, G., Jaupart, C. & Allègre, CJ Nucléation, croissance cristalline et régime thermique des magmas de refroidissement. J. Geophys. Res. Solid Earth 89 , 10161-10177 (1984).
CAS  Article  Google Scholar  

    3.    3.Cashman, KV Relation entre la cristallisation du plagioclase et la vitesse de refroidissement dans les fonds basaltiques. Contrib. Minéral. Essence. 113 , 126–142 (1993).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    4.    4.Vernon, RH et Paterson, SR Quelle est la date de retard des mégacrystes de K-feldspath dans les granites? Lithos 104 , 327–336 (2008).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    5.    5.Chakoumakos, C.-B. & Lumpkin, GR Contraintes pression-température sur la cristallisation de la pegmatite durcissante, comté de Taos, Nouveau-Mexique. Pouvez. Minéral. 28 , 287-298 (1990).
CAS  Google Scholar  

    6.    6.Webber, KL, Simmons, WB, Falster, AU & Foord, EE Taux de refroidissement et dynamique de cristallisation des dykes de pegmatite-aplite peu profonds, comté de San Diego, Californie. Un m. Minéral. 84 , 708–717 (1999).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    7.    sept.London, D. & Morgan, GB Le puzzle de la pegmatite. Elements 8 , 263-268 (2012).
CAS  Article  Google Scholar  

    8.    8.Nabelek, PI, Whittington, AG & Sirbescu, M.-LC Le rôle de H2O dans la mise en place rapide et la cristallisation des pegmatites de granit: résoudre le paradoxe des gros cristaux dans les fonds de fusion hautement sous-refroidis. Contrib. Minéral. Essence. 160 , 313–325 (2010).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    9.    9.Morton, DM, Sheppard, JB, Miller, FK & Lee, C.-TA Petrogenesis of the cogenetic Stewart pegmatite-aplite, Pala, California: Regional implications. Lithosphère 11 , 91–128 (2018).
LES PUBLICITÉS  Article  Google Scholar  

    10.    dix.Jahns, RH & Wright, LA Pegmatites contenant des gemmes et du lithium du district de Pala, comté de San Diego, Californie (État de Californie, Département des ressources naturelles, Division des mines, 1951).

    11.    11.Marshall, DJ & Mariano, AN Cathodoluminescence des matériaux géologiques (Taylor & Francis, 1988).

    12.    12.Götze, J., Plötze, M., Graupner, T., Hallbauer, DK & Bray, CJ Incorporation d'éléments traces dans le quartz: une étude combinée par ICP-MS, résonance de spin électronique, cathodoluminescence, analyse d'ions capillaires et chromatographie en phase gazeuse. Geochim. Cosmochim. Acta 68 , 3741–3759 (2004).
LES PUBLICITÉS  Article  CAS  Google Scholar  

    13.    13.Pearce, NJG et coll. Une compilation de données nouvelles et publiées sur les éléments majeurs et traces pour les matériaux de référence en verre NIST SRM 610 et NIST SRM 612. Geostand. Newsl. 21 , 115–144 (1997).
CAS  Article  Google Scholar  

    14.    14.Savov, IP, Leeman, WP, Lee, C.-TA & Shirey, SB Variations isotopiques du bore dans les rhyolites du nord-ouest des États-Unis: Yellowstone, Snake River Plain, est de l'Oregon. J. Volcanol. Géothermie. Res. 188 , 162-172 (2009).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    15.    15.Götze, J., Plötze, M. & Trautmann, T. Structure et caractéristiques de luminescence du quartz provenant de pegmatites. Un m. Minéral. 90 , 13–21 (2005).
LES PUBLICITÉS  Article  CAS  Google Scholar  

    16.    16.Perny, B., Eberhardt, P., Ramseyer, K., Mullis, J. & Pankrath, R. Microdistribution of Al, Li, and Na in $ α $ quartz: causes possibles et corrélation avec la cathodoluminescence de courte durée. Un m. Minéral. 77 , 534-544 (1992).
CAS  Google Scholar  

    17.    17.Wark, DA & Watson, EB TitaniQ: un géothermomètre en titane dans le quartz. Contrib. Minéral. Essence. 152 , 743–754 (2006).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    18.    18.Huang, R. & Audétat, A. Le thermobaromètre titane-dans-quartz (TitaniQ): un examen critique et un recalibrage. Geochim. Cosmochim. Acta 84 , 75–89 (2012).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    19.    19.Thomas, JB et coll. TitaniQ sous pression: effet de la pression et de la température sur la solubilité du Ti dans le quartz. Contrib. Minéral. Essence. 160 , 743–759 (2010).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    20.    20.Verhoogen, J. Diffusion ionique et conductivité électrique dans le quartz. Un m. Minéral. J. Earth Planet. Mater. 37 , 637–655 (1952).
CAS  Google Scholar  

    21.    21.Tailby, ND, Cherniak, DJ & Watson, diffusion EB Al dans le quartz. Un m. Mineur. 103 , 839-847 (2018).
LES PUBLICITÉS  Article  Google Scholar  

    22.    22.Cherniak, DJ Silicon auto-diffusion en quartz naturel monocristallin et feldspath. Planète Terre. Sci. Lett. 214 , 655–668 (2003).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    23.    23.Rubin, AE et coll. Refroidissement rapide et stockage à froid dans un réservoir de magma silicique enregistré dans des cristaux individuels. Science 356 , 1154-1156 (2017).
CAS  PubMed  Article  PubMed Central  Google Scholar  

    24.    24.Tang, M., Rudnick, RL, McDonough, WF, Bose, M. & Goreva, Y. Diffusion de Li multimode dans les zircons naturels: preuve de la diffusion en présence de limites de concentration en fonction d'étape. Planète Terre. Sci. Lett. 474 , 110–119 (2017).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    25.    25.Nash, WP & Crecraft, HR Coefficients de partage pour les éléments traces dans les magmas siliciques. Geochim. Cosmochim. Acta 49 , 2309-2322 (1985).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    26.    26.Neukampf, J., Ellis, BS, Magna, T., Laurent, O. & Bachmann, O. Partitionnement et fractionnement isotopique du lithium dans les phases minérales des rhyolites chaudes et sèches: le cas du Mesa Falls Tuff, Yellowstone. Chem. Geol. 506 , 175-186 (2019).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    27.    27.Shannon, RD & Prewitt, CT Valeurs révisées des rayons ioniques effectifs. Acta Crystallogr. Secte. B 26 , 1046-1048 (1970).
CAS  Article  Google Scholar  

    28.    28.Wells, AF Structural Inorganic Chemistry (Oxford Univ. Press, 2012).

    29.    29.Drewitt, JWE et coll. Structure du verre GeO2 à des pressions allant jusqu'à 8,6 GPa. Phys. Rev. B 81 , 14202 (2010).
LES PUBLICITÉS  Article  CAS  Google Scholar  

    30.    30.He, D., Lee, C.-TA, Yu, X. & Farner, M. Ge / Si partitionnement dans les systèmes ignés: contraintes de l'ablation laser mesures ICP-MS sur des échantillons naturels. Geochem. Geophys. Geosystems 20 , 4472–4486 (2019).

    31.    31.Tiller, WA, Jackson, KA, Rutter, JW & Chalmers, B. La redistribution des atomes de soluté lors de la solidification des métaux. Acta Met. 1 , 428–437 (1953).
CAS  Article  Google Scholar  

    32.    32.Burton, JA, Prim, RC & Slichter, WP La distribution du soluté dans les cristaux issus de la fusion. Partie I. Théorique. J. Chem. Phys. 21 , 1987–1991 (1953).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    33.    33.Watson, EB & Müller, T. Fractionnement isotopique et élémentaire hors équilibre pendant la croissance cristalline contrôlée par diffusion dans des conditions statiques et dynamiques. Chem. Geol. 267 , 111-124 (2009).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    34.    34.Smith, VG, Tiller, WA & Rutter, J. Une analyse mathématique de la redistribution des solutés pendant la solidification. Pouvez. J. Phys. 33 , 723–745 (1955).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    35.    35.Glicksman, ME Principes de solidification: une introduction aux concepts de moulage moderne et de croissance cristalline (Springer Science & Business Media, 2010).

    36.    36.DePaolo, DJ Modèle cinétique de surface pour le fractionnement isotopique et d'oligo-éléments lors de la précipitation de calcite à partir de solutions aqueuses. Geochim. Cosmochim. Acta 75 , 1039–1056 (2011).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    37.    37.Hofmann, AW, Jochum, KP, Seufert, M. & White, WM Nb et Pb dans les basaltes océaniques: nouvelles contraintes sur l'évolution du manteau. Planète Terre. Sci. Lett. 79 , 33–45 (1986).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    38.    38.Jahns, RH & Burnham, CW Études expérimentales de la genèse de la pegmatite; l, Un modèle pour la dérivation et la cristallisation des pegmatites granitiques. Econ. Geol. 64 , 843–864 (1969).
CAS  Article  Google Scholar  

    39.    39.London, D. Processus de formation de minerai dans les pegmatites granitiques. Ore Geol. Rev. 101 , 349-383 (2018).
Article  Google Scholar  

    40.    40.Fournier, RO & Potter, RW II Une équation corrélant la solubilité du quartz dans l'eau de 25 à 900 C à des pressions allant jusqu'à 10 000 bars. Geochim. Cosmochim. Acta 46 , 1969-1973 (1982).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    41.    41.Burnham, CW, Holloway, JR & Davis, NF Le volume spécifique d'eau dans la plage de 1000 à 8900 bars, 20 à 900 C. Am. J. Sci. 267 , 70–95 (1969).
CAS  Google Scholar  

    42.    42.Nigrini, A. Diffusion dans les systèmes d'altération des roches; I, Prédiction de limiter les conductances ioniques équivalentes à des températures élevées. Un m. J. Sci. 269 , 65–91 (1970).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    43.    43.Yuan-Hui, L. & Gregory, S. Diffusion d'ions dans l'eau de mer et dans les sédiments des grands fonds. Geochim. Cosmochim. Acta 38 , 703–714 (1974).
LES PUBLICITÉS  Article  Google Scholar  

    44.    44.Zhang, J. & Lee, C.-TA Cristallisation de déséquilibre et croissance rapide des cristaux: une étude de cas de granitoïdes orbiculaires d'origine magmatique. Int. Geol. Rév . https://doi.org/10.1080/00206814.2020.1734975 , 1-17 (2020).

    45.    45.Vance, D. & O'nions, RK Chronométrie isotopique des grenats zonés: cinétique de croissance et histoires métamorphiques. Planète Terre. Sci. Lett. 97 , 227-240 (1990).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    46.    46.Dragovic, B., Baxter, EF & Caddick, MJ Déshydratation pulsée et croissance du grenat pendant la subduction révélées par la géochronologie zonée du grenat et la modélisation thermodynamique, Sifnos, Grèce. Planète Terre. Sci. Lett. 413 , 111-122 (2015).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    47.    47.Swanson, SE Relation entre la nucléation et le taux de croissance cristalline et le développement de textures granitiques. Un m. Minéral. 62 , 966–978 (1977).
CAS  Google Scholar  

    48.    48.Gualda, GAR et coll. Échelles de temps de la cristallisation du quartz et de la longévité du corps magmatique géant Bishop. PLoS ONE 7 , e37492 (2012).
LES PUBLICITÉS  CAS  PubMed  PubMed Central  Article  Google Scholar  

    49.    49.Pamukcu, AS, Ghiorso, MS & Gualda, GAR Jantes High-Ti, bright-CL en quartz volcanique: résultat d'une croissance très rapide. Contrib. Minéral. Essence. 171 et 105 (2016).
LES PUBLICITÉS  Article  CAS  Google Scholar  

    50.    50.DeMets, C., Gordon, RG, Argus, DF & Stein, S. Mouvements actuels de la plaque. Geophys. J. Int. 101 , 425–478 (1990).
LES PUBLICITÉS  Article  Google Scholar  

    51.    51.Rowe, CD & Griffith, WA Les failles Do préservent un record de glissement sismique: un deuxième avis. J. Struct. Geol. 78 , 1–26 (2015).
LES PUBLICITÉS  Article  Google Scholar  

    52.    52.Wilson, LO Sur l'interprétation d'une grandeur dans l'équation de Burton, Prim et Slichter comme une épaisseur de couche limite de diffusion. J. Cryst. Growth 44 , 247–250 (1978).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    53.    53.Voloshin, AE, Prostomolotov, AI & Verezub, NA Sur la précision des modèles analytiques de la ségrégation des impuretés pendant la cristallisation directionnelle en fusion et leur applicabilité pour les calculs quantitatifs. J. Cryst. Growth 453 , 188–197 (2016).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    54.    54.Turcotte, DL et Schubert, G. Geodynamics (Cambridge Univ. Press, 2002).

    55.    55.Zhang, Y. & Xu, Z. Cinétique de la dissolution et de la fusion des cristaux par convection, avec des applications à la dissolution et à la dissociation des hydrates de méthane dans l'eau de mer. Planète Terre. Sci. Lett. 213 , 133-148 (2003).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    56.    56.Kerr, RC Dissolution cristalline par convection. Contrib. Minéral. Essence. 121 , 237–246 (1995).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    57.    57.Kundu, PK, Cohen, IM & Dowling, DR Fluid Mechanics (Elsevier Science, 2012).

    58.    58.Behrens, H. & Zhang, Y. Diffusion de l'ar dans les fondus siliciques hydratés: implications pour les mécanismes de diffusion volatile et le fractionnement. Planète Terre. Sci. Lett. 192 , 363 à 376 (2001).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    59.    59.Watson, EB Diffusion de CO 2 et Cl dissous dans la silicique hydratée vers les magmas intermédiaires. Geochim. Cosmochim. Acta 55 , 1897-1902 (1991).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    60.    60.Ackerson, MR, Tailby, ND & Watson, EB Les éléments traces dans le quartz éclairent la provenance des sédiments. Geochem. Geophys. Geosyst. 16 , 1894-1904 (2015).
LES PUBLICITÉS  CAS  Article  Google Scholar  

    61.    61.Garate-Olave, I., Müller, A., Roda-Robles, E., Gil-Crespo, PP & Pesquera, A. Fractionnement extrême dans un système granite-pegmatite documenté par chimie du quartz: l'étude de cas de Tres Arroyos (Centre Zone ibérique, Espagne). Lithos 286 , 162–174 (2017).
LES PUBLICITÉS  Article  CAS  Google Scholar  

    62.    62.Peacock, JM Température et croissance des feuilles chez quatre espèces de graminées. J. Appl. Ecol . 13 , 225-232 (1976).


Remerciements

Ce travail a été soutenu par NSF-EAR 1753599 à C.-TAL Les discussions avec Hehe Jiang, Ming Tang, Eytan Sharton-Bierig, Julin Zhang et Blue Sheppard sont appréciées.

Informations sur l'auteur/Affiliations

    1.    Department of Earth, Environmental and Planetary Sciences, Rice University, Houston, TX, 77005, USA
Patrick R. Phelps et Cin-Ty A. Lee

    2.    Department of Earth and Planetary Sciences, University of California, Riverside, CA, 92521, USA
Douglas M. Morton


Contributions

PRP a analysé des échantillons, fourni une interprétation et participé à l'écriture. C.-TAL a aidé à l'interprétation et à l'écriture. DMM a fourni des échantillons et un contexte géologique.
auteur correspondant
Correspondance adressée à Patrick R. Phelps .

Déclarations éthiques /Intérêts concurrents

Les auteurs ne déclarent aucun intérêt concurrent.

Information additionnelle

Information sur l'examen par les pairs Nature Communications remercie Andrea Dini et les autres évaluateurs anonymes pour leur contribution à l'examen par les pairs de ce travail. Les rapports des pairs évaluateurs sont disponibles.
Note de l'éditeur Springer Nature reste neutre en ce qui concerne les revendications juridictionnelles dans les cartes publiées et les affiliations institutionnelles.

Résumé d'une phrase : Les distributions d'éléments traces de cristaux de quartz pegmatitiques indiquent une croissance rapide dans des environnements hautement dynamiques, ce qui suggère que des cristaux à grande échelle peuvent se former en quelques jours.

Droits et permissions

Accès libre Cet article est concédé sous une licence internationale Creative Commons Attribution 4.0, qui permet l'utilisation, le partage, l'adaptation, la distribution et la reproduction dans n'importe quel support ou format, à condition que vous accordiez le crédit approprié aux auteurs originaux et à la source, fournir un lien vers la licence Creative Commons et indiquer si des modifications ont été apportées. Les images ou tout autre matériel tiers dans cet article sont inclus dans la licence Creative Commons de l'article, sauf indication contraire dans une ligne de crédit pour le matériel. Si le matériel n'est pas inclus dans la licence Creative Commons de l'article et que votre utilisation prévue n'est pas autorisée par la réglementation statutaire ou dépasse l'utilisation autorisée, vous devrez obtenir la permission directement du détenteur des droits d'auteur. Pour voir une copie de cette licence, visitezhttp://creativecommons.org/licenses/by/4.0/ .

Source de l'article en anglais :

https://www.nature.com/articles/s41467-020-18806-w